FineKernelToolKit 4.2.13
読み取り中…
検索中…
一致する文字列を見つけられません
公開メンバ関数 | プロパティ | 全メンバ一覧
FK_CLI::fk_Gregory クラス

Gregory 曲面を生成、管理するクラス [詳解]

#include <CLI/FK_CLI/include/Gregory_CLI.h>

+ FK_CLI::fk_Gregory の継承関係図
+ FK_CLI::fk_Gregory 連携図

公開メンバ関数

 fk_Gregory (void)
 コンストラクタ
 
 ~fk_Gregory ()
 デストラクタ
 
 !fk_Gregory ()
 ファイナライザ
 
void Init (void)
 初期化用メソッド
 
bool SetBoundary (fk_UV uv, int vID, fk_Vector^ pos)
 境界制御点設定メソッド
 
bool SetDerivative (fk_UV uv, int vID, fk_Vector^ pos)
 流れベクトル制御点設定メソッド
 
fk_Vector ^ GetBoundary (fk_UV uv, int vID)
 境界制御点参照メソッド
 
fk_Vector ^ GetDerivative (fk_UV uv, int vID)
 流れベクトル制御点参照メソッド
 
void AdjustDerivative (void)
 流れベクトル制御点自動設定メソッド
 
void AdjustDerivative (fk_UV uv)
 境界別流れベクトル制御点自動設定メソッド
 
bool Connect (fk_Gregory^ surf, fk_UV thisUV, fk_UV otherUV, bool d, bool mode)
 隣接曲面G1連続接続メソッド
 
fk_Vector ^ Pos (double u, double v)
 曲面点算出メソッド
 
fk_Vector ^ Norm (double u, double v)
 曲面法線ベクトル算出メソッド
 
fk_Vector ^ UDeriv (double u, double v)
 曲面 u 方向偏微分ベクトル算出メソッド
 
fk_Vector ^ VDeriv (double u, double v)
 曲面 v 方向偏微分ベクトル算出メソッド
 
- 基底クラス FK_CLI::fk_Shape に属する継承公開メンバ関数
void SetShaderAttribute (String^ name, int dim, IEnumerable< int >^ array)
 シェーダー内 attribute 変数設定メソッド1
 
void SetShaderAttribute (String^ name, int dim, IEnumerable< float >^ array)
 シェーダー内 attribute 変数設定メソッド2
 
void SetShaderAttribute (String^ name, int dim, IEnumerable< double >^ array)
 シェーダー内 attribute 変数設定メソッド3
 
void SetShaderAttribute (String^ name, int dim, IEnumerable< fk_Vector^>^ array)
 シェーダー内 attribute 変数設定メソッド4
 
void SetShaderAttribute (String^ name, int dim, IEnumerable< fk_TexCoord^>^ array)
 シェーダー内 attribute 変数設定メソッド5
 
void SetShaderAttribute (String^ name, int dim, IEnumerable< fk_HVector^>^ array)
 シェーダー内 attribute 変数設定メソッド6
 
- 基底クラス FK_CLI::fk_Attribute に属する継承公開メンバ関数
bool SetAttrII (int key, int value)
 キーが int 型、値が int 型である属性設定メソッド
 
bool SetAttrID (int key, double value)
 キーが int 型、値が double 型である属性設定メソッド
 
bool SetAttrIS (int key, String^ value)
 キーが int 型、値が String 型である属性設定メソッド
 
bool SetAttrSI (String^ key, int value)
 キーが String 型、値が int 型である属性設定メソッド
 
bool SetAttrSD (String^ key, double value)
 キーが String 型、値が double 型である属性設定メソッド
 
bool SetAttrSS (String ^ key, String^ value)
 キーが String 型、値が String 型である属性設定メソッド
 
int GetAttrII (int key)
 キーが int 型、値が int 型である属性参照メソッド
 
double GetAttrID (int key)
 キーが int 型、値が double 型である属性参照メソッド
 
String ^ GetAttrIS (int key)
 キーが int 型、値が String 型である属性参照メソッド
 
int GetAttrSI (String^ key)
 キーが String 型、値が int 型である属性参照メソッド
 
double GetAttrSD (String^ key)
 キーが String 型、値が double 型である属性参照メソッド
 
String ^ GetAttrSS (String^ key)
 キーが String 型、値が String 型である属性参照メソッド
 
bool ExistAttrII (int key)
 キーが int 型、値が int 型である属性存在参照メソッド
 
bool ExistAttrID (int key)
 キーが int 型、値が double 型である属性存在参照メソッド
 
bool ExistAttrIS (int key)
 キーが int 型、値が String 型である属性存在参照メソッド
 
bool ExistAttrSI (String^ key)
 キーが String 型、値が int 型である属性存在参照メソッド
 
bool ExistAttrSD (String^ key)
 キーが String 型、値が double 型である属性存在参照メソッド
 
bool ExistAttrSS (String^ key)
 キーが String 型、値が String 型である属性存在参照メソッド
 
bool DeleteAttrII (int key)
 キーが int 型、値が int 型である属性消去メソッド
 
bool DeleteAttrID (int key)
 キーが int 型、値が double 型である属性消去メソッド
 
bool DeleteAttrIS (int key)
 キーが int 型、値が String 型である属性消去メソッド
 
bool DeleteAttrSI (String^ key)
 キーが String 型、値が int 型である属性消去メソッド
 
bool DeleteAttrSD (String^ key)
 キーが String 型、値が double 型である属性消去メソッド
 
bool DeleteAttrSS (String^ key)
 キーが String 型、値が String 型である属性消去メソッド
 

プロパティ

int Div [get, set]
 分割数プロパティ
 
- 基底クラス FK_CLI::fk_Shape に属する継承プロパティ
fk_RealShapeType^ RealShapeType [get]
 形状データ構造プロパティ
 

詳解

Gregory 曲面を生成、管理するクラス

このクラスは、形状として Gregory 曲面を制御する機能を提供します。 u,v 両方向で 3 次式のみに対応しています。

Gregory 曲面の境界線や制御点は以下の図のような構成を持っています。

Gregory曲面の構成

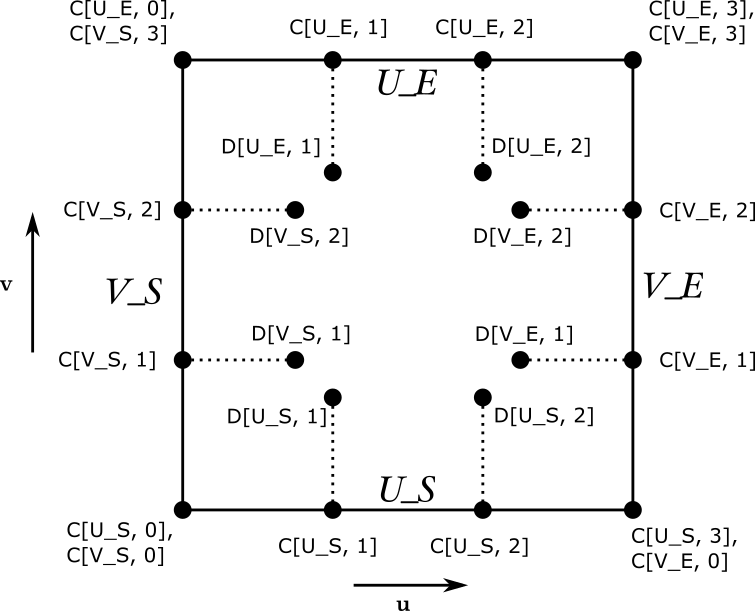
以降、この図に基づいて各要素を解説していきます。

Gregory 曲面の境界は以下のような 4 本の 3 次 Bezier 曲線により構成されています。

これらの境界線を構成する制御点を「境界制御点」と呼び、 図中の「C」で構成されている制御点にあたります。 これらの点位置は setBoundary() で設定が可能で、 「曲線名」と「ID」によって指定します。 図中の境界制御点の一番目が曲線名、二番目が ID にあたります。 4隅の制御点については指定方法が 2 種類あります。 例えば、図の左上の制御点は SetBoundary(fk_UV.U_E, 0, V) と SetBoundary(fk_UV.V_S, 3, V) の両方の指定方法があります。

Gregory 曲面は境界制御点の他に、流れベクトルを制御する 「流れベクトル制御点」があり、図中の「D」で構成されている点にあたります。 これらの制御点の位置を変更しても境界線は変化しませんが、 曲面境界部分の流れベクトル(偏微分ベクトル)が変化します。 流れベクトルを適切に設定すると、 隣り合う曲面が境界部分で折れ曲がらず滑らかに接続することができます。

構築子と解体子

◆ fk_Gregory()

FK_CLI::fk_Gregory::fk_Gregory ( void  )

コンストラクタ

◆ ~fk_Gregory()

FK_CLI::fk_Gregory::~fk_Gregory ( )

デストラクタ

◆ !fk_Gregory()

FK_CLI::fk_Gregory::!fk_Gregory ( )

ファイナライザ

関数詳解

◆ Init()

void FK_CLI::fk_Gregory::Init ( void  )

初期化用メソッド

このメソッドは、曲面を初期状態(全ての制御点が原点にある状態)にします。

◆ SetBoundary()

bool FK_CLI::fk_Gregory::SetBoundary ( fk_UV  uv,
int  vID,
fk_Vector^  pos 
)

境界制御点設定メソッド

境界線の制御点位置ベクトルを設定します。

引数
[in]uv設定を行う境界線の種類
[in]vID制御点 ID。先頭は 0 になります。
[in]pos制御点位置ベクトル
戻り値
設定に成功した場合 true、失敗した場合 false を返します。

◆ SetDerivative()

bool FK_CLI::fk_Gregory::SetDerivative ( fk_UV  uv,
int  vID,
fk_Vector^  pos 
)

流れベクトル制御点設定メソッド

流れベクトル制御点位置ベクトルを設定します。

引数
[in]uv設定を行う境界線の種類
[in]vID制御点 ID。1, 2 のいずれかになります。
[in]pos制御点位置ベクトル
戻り値
設定に成功した場合 true、失敗した場合 false を返します。

◆ GetBoundary()

fk_Vector ^ FK_CLI::fk_Gregory::GetBoundary ( fk_UV  uv,
int  vID 
)

境界制御点参照メソッド

曲面の境界制御点位置ベクトルを参照します。

引数
[in]uv境界線種類
[in]vID制御点のv方向ID
戻り値
制御点位置ベクトル。IDが不正だった場合、零ベクトルを返します。

◆ GetDerivative()

fk_Vector ^ FK_CLI::fk_Gregory::GetDerivative ( fk_UV  uv,
int  vID 
)

流れベクトル制御点参照メソッド

曲面の流れベクトル制御点位置ベクトルを参照します。

引数
[in]uv境界線種類
[in]vID制御点のv方向ID
戻り値
制御点位置ベクトル。IDが不正だった場合、零ベクトルを返します。

◆ AdjustDerivative() [1/2]

void FK_CLI::fk_Gregory::AdjustDerivative ( void  )

流れベクトル制御点自動設定メソッド

現在の境界曲線情報より、流れベクトル制御点を自動的に設定します。 このとき、内部制御点は境界上の流れベクトルが線形補間となるように設定されます。

参照
AdjustDerivative(fk_UV), SetBoundary(), SetDerivative(), Connect()

◆ AdjustDerivative() [2/2]

void FK_CLI::fk_Gregory::AdjustDerivative ( fk_UV  uv)

境界別流れベクトル制御点自動設定メソッド

特定の境界線に対し、現在の境界曲線情報より流れベクトル制御点を自動的に設定します。 このとき、流れベクトル制御点は境界上の流れベクトルが線形補間となるように設定されます。

引数
[in]uv指定する制御点に隣接する境界曲線を指定します。
参照
AdjustDerivative(void), SetBoundary(), SetDerivative(), Connect()

◆ Connect()

bool FK_CLI::fk_Gregory::Connect ( fk_Gregory^  surf,
fk_UV  thisUV,
fk_UV  otherUV,
bool  d,
bool  mode 
)

隣接曲面G1連続接続メソッド

隣接する曲面と G1 連続性を持つように制御点位置を移動します。 隣接する境界線のうち、両端点については一致している必要があります。 その他の制御点については、 surf 側の制御点に従って補正が行われます。

引数
[in]surf隣接曲面。 隣接している境界線の両端点が一致している必要があります。
[in]thisUV接続する境界曲線を指定します。
[in]otherUVsurf 側の接続境界曲線を指定します。
[in]d自身と surf の境界が同じ方向になる場合 true を、 逆方向になる場合 false を代入します。
[in]mode連続性を C1 とするか G1 とするかを設定します。 C1 連続とは、境界上の流れベクトルが全て連続であることです。 一方、G1 連続とは境界上の接平面が連続であることです。 G1 連続は必ずしも流れベクトルが連続である必要はありません。

true の場合、C1 連続性を持つように制御点を移動します。 false の場合、G1 連続性を持つように制御点を移動します。

戻り値
接続に成功した場合 true を、失敗した場合 false を返します。
参照
SetBoundary(), SetDerivative(), AdjustDerivative(void), AdjustDerivative(fk_UV)

◆ Pos()

fk_Vector ^ FK_CLI::fk_Gregory::Pos ( double  u,
double  v 
)

曲面点算出メソッド

パラメータに対応する曲面上の点の位置ベクトルを返します。

引数
[in]u曲面の u パラメータ
[in]v曲面の v パラメータ
戻り値
曲面上の点の位置ベクトル

◆ Norm()

fk_Vector ^ FK_CLI::fk_Gregory::Norm ( double  u,
double  v 
)

曲面法線ベクトル算出メソッド

曲面上の法線ベクトルを返します。

引数
[in]uu パラメータ
[in]vv パラメータ
戻り値
曲面上の法線ベクトル

◆ UDeriv()

fk_Vector ^ FK_CLI::fk_Gregory::UDeriv ( double  u,
double  v 
)

曲面 u 方向偏微分ベクトル算出メソッド

曲面上の u 方向偏微分ベクトルを算出する関数です。

引数
[in]uu パラメータ
[in]vv パラメータ
戻り値
曲面上の u 方向偏微分ベクトル

◆ VDeriv()

fk_Vector ^ FK_CLI::fk_Gregory::VDeriv ( double  u,
double  v 
)

曲面 v 方向偏微分ベクトル算出メソッド

曲面上の v 方向偏微分ベクトルを算出する関数です。

引数
[in]uu パラメータ
[in]vv パラメータ
戻り値
曲面上の v 方向偏微分ベクトル

プロパティ詳解

◆ Div

int FK_CLI::fk_Gregory::Div
getset

分割数プロパティ

このプロパティは、描画時分割数の設定や参照に使用します。

構築: doxygen 1.9.8